欧拉函数与欧拉定理

数论 1 Minute

欧拉函数

定义

1-N中与N互质的的数的个数被称为N的欧拉函数，记作\phi (N).

计算

在算术基本定理中，N=p_1^{c_1}p_2^{c_2} \cdots p_m^{c_m}.
若p_i,p_j是N的质因子，由容斥原理得1-N中，p_i或p_j的倍数个数为\frac{N}{p_i}+\frac{N}{p_j}-\frac{N}{p_ip_j}.
因此，
\phi(N)=N*\prod_{i=1}^m(1-\frac{1}{p_i})

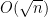O(\sqrt{n})朴素单点求值

ll getPhi(ll n)
{
  ll ans=n;
  for (l i=2;i*i<=n;i++) {
    if (n%i==0) {
      ans=ans/i*(n-i);
      while (n%i==0) {
        n/=i;
      }
    }
  }
  if (n>1) {
    ans=ans/n*(n-1);
  }
  return ans;
}

线性筛

#include<bits/stdc++.h>
using namespace std;

const int MAXN=(int)1e7+10;

int v[MAXN],prime[MAXN],phi[MAXN];

void Euler(int n);

int main()
{
  Euler((int)1e7);
  return 0;
}

void Euler(int n)
{
  int m=0;
  for (int i=2;i<=n;i++) {
    if (v[i]==0) {
      v[i]=i;
      prime[++m]=i;
      phi[i]=i-1;
    }
  
    for (int j=1;j<=m;j++) {
      if (prime[j]>v[i] || prime[j]>n/i) {
        break;
      }
      v[i*prime[j]]=prime[j];
      phi[i*prime[j]]=phi[i]*(i%prime[j] ? prime[j]-1 : prime[j]);
    }
  }
  prime[0]=m;
}

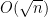O(\sqrt{n})预处理,O(\frac{\sqrt{n}}{logn})单点求值

ll getPhi(ll n)
{
  if (n<MAXN) {
    return phi[n];
  }
  ll ans=n;
  for (int i=1;i<=prime[0] && prime[i]*prime[i]<=n;i++) {
    if (n%prime[i]==0) {
      ans=ans/prime[0]*(prime[0]+1);
      while (n%prime[i]==0) {
        n/=prime[i];
      }
    }
  }
  if (n>1) {
    ans=ans/n*(n-1);
  }
  return ans;
}

欧拉定理

若\gcd(a,m)=1 , a^n\equiv a^{n\mod \phi(m)}\mod m

广义欧拉定理

a^n\equiv a^{n\mod \phi(m)}\mod m , n<\phi(m)
a^n\equiv a^{n\mod \phi(m)+phi(m)}\mod m , n\geq \phi(m)

未知 的头像

发布者：风竹曦

已发布

留下评论